
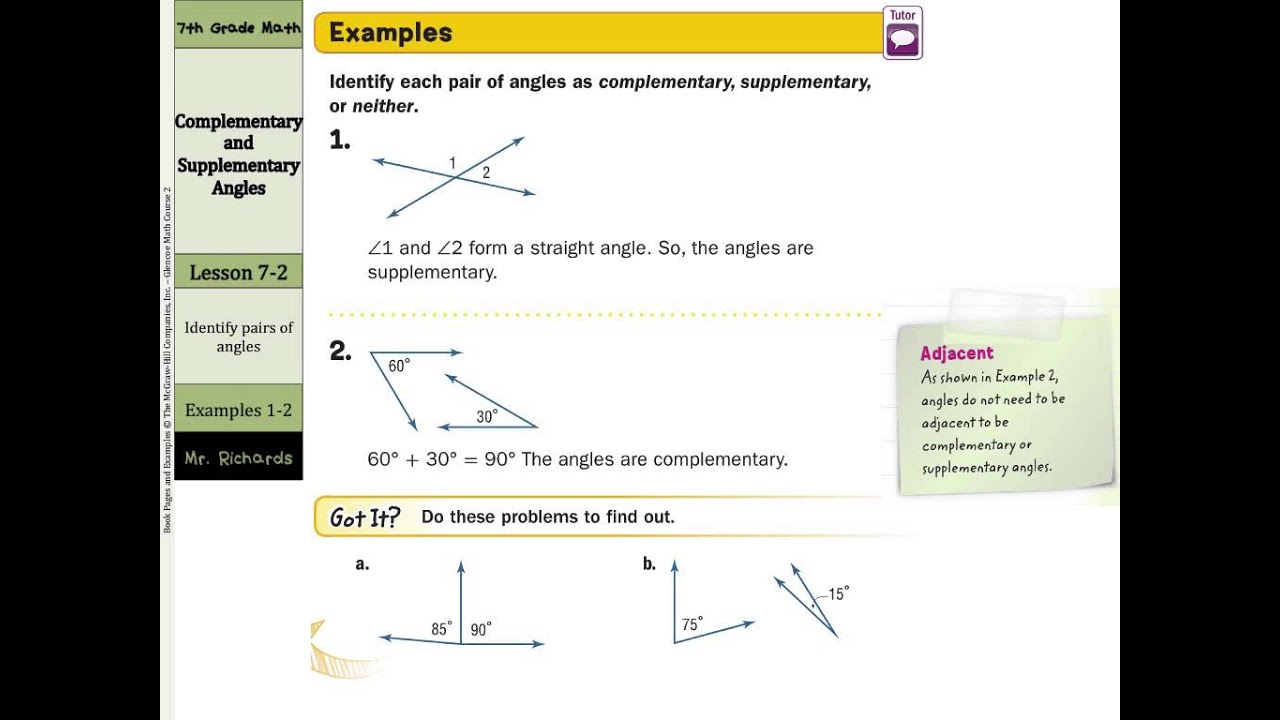
Find x if these angles are supplementary angles.Find n and the missing angle if these angles are complementary angles.Find x if these angles are complementary angles.
It willĪlso explain a neat trick to remember the difference between complementary and supplementary angles. This video describes complementary and supplementary angles with a few example problems.
#Complement angle and supplementary angle how to
Have a look at the following videos for further explanations of complementary angles and supplementaryĪngles: How To Identify And Differentiate Complementary And Supplementary Angles? The S in Supplementary stands for Straight, 180˚ Video Lessons The C in Complementary stands for Corner, 90˚ If the two supplementary angles are adjacent then they will form a straight line.

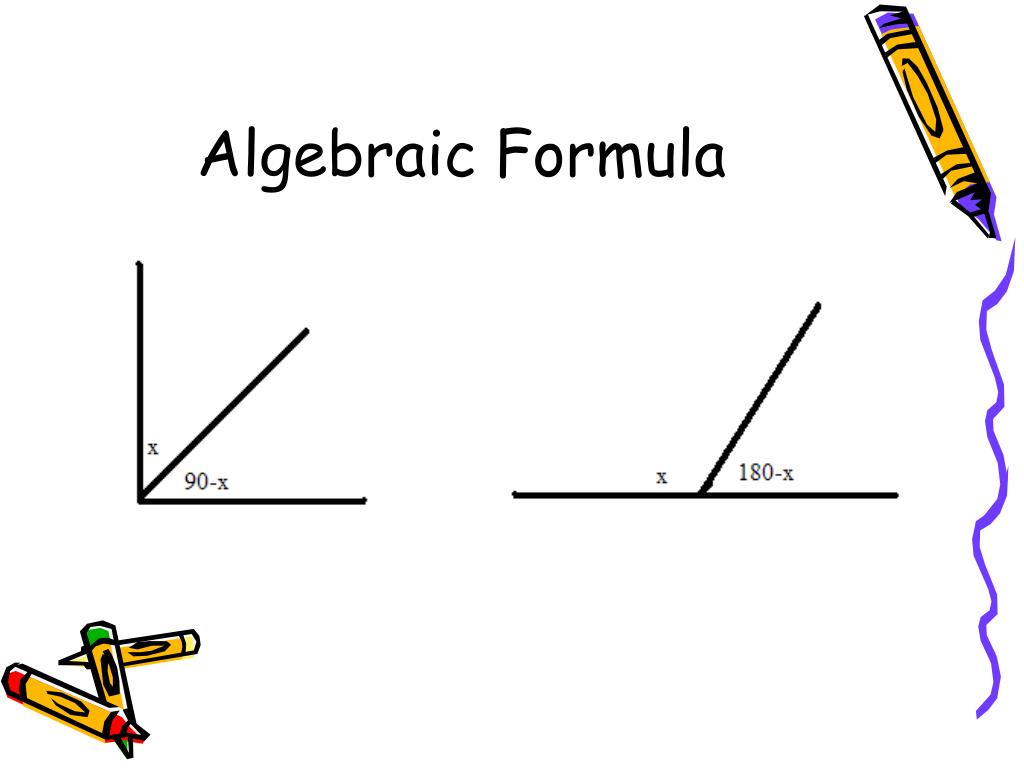
The two angles do not need to be together or adjacent. One of the supplementary angles is said to be the supplement of the other. Two angles are called supplementary angles if the sum of their degree measurements equals 180 degrees (straight line). Therefore, the other two angles must add up to 90˚. This is because the sum of angles in a triangle is 180˚ and the right angle is 90˚. In a right triangle, the two acute angles are complementary. Two complementary angles are adjacent then they will form a right angle. One of the complementary angles is said to Their degree measurements equals 90 degrees (right angle). Two angles are called complementary angles if the sum of If you need more explanations about complementary and supplementary angles, videos and worksheets. So remember that when you're trying to evaluate your problems that supplementary sum to 180 degrees or they're linear and complementary angles sum to 90 degrees.The following table gives a summary of complementary and supplementary angles. So notice that for a supplementary and for complementary you can't say that five angles are complementary but we're always talking about pairs or two's.
Now, a supplementary pair could be angle 4 and angle 5 which are adjacent and they are linear. So complementary angles could be angles 1 and 2. Here we have five angles 1, 2, 3, 4 and 5 and we're told that this angle 3 is 90 degrees, now one thing that you can assume is that 1, 2 and 3 are all linear, so if you add up 1, 2 and 3 it would be 180 degrees, which means that 1 and 2 must also sum to 90 degrees so I could label this as a right-angle. Let's look at a specific example where you might be asked to identify supplementary angles and complementary angles. The same is true for complementary angles. But I could also say if we had some angle here that we said three and let's say 3 was equal to 60 degrees and I had some other angle over here, let's say angle four was equal to 120 degrees, I could say that these two angles three and four are supplementary because they sum to 180 degrees. So supplementary angles could be adjacent so if I had angles one and two those two would be supplementary.

And I noted here that these do not have to be adjacent. Supplementary angles are two angles whose measures sum to a 180 degrees and complementary are the sum have to add up to 90 degrees. Two concepts that are related but not the same are supplementary angles and complementary angles.


 0 kommentar(er)
0 kommentar(er)
